| Fermeture fenêtre |
Etude des concentrations d'aspects planétaires à la naissance d'individus appartenant à différents groupes professionnels
Etude statistique effectuée à partir de documents fournis par Michel Gauquelin. Laboratoire d’Etude des Relations entre Rythmes Cosmiques et Psychophysiologiques 8 rue Amyot, 75005 PARIS, 1989.
1. Introduction
Les statistiques qui sont présentées dans cet article ont pour but de mettre en évidence des corrélations intéressantes existant entre les naissances des individus ayant exercé dans leur vie certaines professions, et le moment où ont eu lieu certains phénomènes astronomiques mettant en jeu un astre particulier du système solaire.
L'objet principal de cette étude est de montrer que ces résultats se maintiennent très bien malgré une analyse sévère tendant à balayer toute cause de biais de nature astronomique, sociale, démographique ou autre, ce qui pose la question d'un éventuel bien-fondé de l'idée astrologique.
Le travail exposé ici a été accompli en 1989 grâce à l'utilisation d'un micro-ordinateur très puissant (80386+87 / 2OMH) pour l’époque, et aurait donc été très coûteux il y a seulement quelques années, requérant toute la puissance d'un centre de calcul, généralement réservée à des recherches sérieusement financées.
L'informatique permet ainsi aujourd'hui la mise en œuvre de méthodes d'investigation statistiques assez lourdes, donnant accès à toute la richesse des informations potentiellement contenues dans les considérables recueils de dates et heures de naissances, réunis avec une patience infinie par le chercheur Michel Gauquelin depuis maintenant quatre décennies.
C'est l'une de ces méthodes, conçue par l'auteur, qui est exposée ici et baptisée :
"Méthode des concentrations d'aspects planétaires"
2. Principe de la méthode de calcul
Pour chaque thème d'un groupe professionnel donné sont calculées les concentrations d'aspects, définies plus loin dans le texte, de chaque planète de ce thème. Lorsqu'une de ces concentrations dépasse un certain seuil, la planète concernée est considérée comme "valorisée" et son score de groupe est incrémenté d'une unité.
Ces scores sont ensuite évalués par rapport aux scores d'un groupe de référence qui est constitué par plusieurs dizaines de milliers de thèmes de naissances fictifs dont les dates et heures sont distribués aléatoirement aux environs des dates et heures de naissance réelles du groupe étudié, d'une façon telle que les trois effets principaux jouant sur les résultats (distribution journalière non homogène, effet saisonnier et concentration planétaire dans la génération des groupes testés) sont rendus inopérants (leur effet résiduel est-il du moins rendu négligeable).
La constitution de ces scores de référence fictifs est le point le plus délicat de la méthode. La démarche proposée ici, qui est particulièrement gourmande en temps de calcul, d'où l'emploi d'un ordinateur très rapide, garantit en contrepartie un haut degré de fiabilité des scores de référence, reposant sur leur convergence vers des limites théoriques exactes lorsque le nombre d'échantillons aléatoires tend vers l'infini.
3. Définition et calcul des concentrations d'aspects
Retenons comme constituants d'une carte du ciel de la naissance d'un individu, adoptant l'habituelle projection sur l'écliptique et le centre de référence terrestre, les douze points principaux suivants:
• Les dix planètes (au sens large) c'est à dire le soleil, la lune, mercure, vénus, mars, jupiter, satume, uranus, neptune et pluton.
• Les deux points terrestres constitués par l'intersection de l'horizon et du méridien du lieu avec le cercle écliptique, qui sont nommés respectivement l'ascendant et le milieu du ciel.
Nous nous intéressons dans cette méthode aux angles formés par chaque couple de points par rapport à la terre:
En premier lieu la conjonction, considérée par les astronomes comme phénomène remarquable (angle proche de zéro) et par les astrologues comme déterminant le plus puissant rapport entre les deux symboles associés (angle inférieur à dix ou douze degrés)
En second lieu les quatre aspects majeurs suivants: l'opposition (180°), le trigone (120°), le carré (90°) et le sextile (60°).
La discipline astrologique considère qu'il existe un aspect entre deux positions astronomiques lorsque la différence de l'angle formé entre elles et de l'aspect exact ne dépasse pas une valeur appelée orbe, et chiffrée en fonction de l'importance symbolique de l'aspect (par exemple: 10 ou 12 degrés pour la conjonction, 5 ou 6 pour le sextile).
Cette convention qui a pour mérite d'être simple, est insatisfaisante lorsqu'un aspect est proche de la limite de l'orbe ou inversement: le passage brutal de son "abandon" à son entière prise en compte, s'il n'ennuie pas l'astrologue rompu aux considérations subjectives savamment dosées, est plutôt gênant dans une démarche rationnelle et systématique attachée à éliminer le maximum de paramètres arbitraires.
Aussi nous nous appliquerons à affecter à chaque aspect un coefficient, nommé coefficient d'aspect, variant de 0 à 1 en raison de sa plus ou moins grande exactitude, et assorti d'une orbe très large, écart pour lequel ce coefficient est nul.
Voici les orbes que nous avons choisi:
• 16° pour les conjonctions et oppositions.
• 8° pour les trigones, carrés et sextiles.
Ce dernier choix (8°) se justifie par le fait que les trigones, carrés et sextiles se forment deux fois plus souvent que les conjonctions et oppositions (2 par cycle).
Ainsi le coefficient d'aspect d'une conjonction limite d'un point de vue astrologique (orbe=12°) serait-il égal à (16-12)/16 c'est-à-dire 0.25, ce qui impliquerait en l’occurrence que la conjonction limite serait quatre fois moins significative que la conjonction exacte!
Précisons que cette nouvelle quantification, bien qu'arbitraire, l'est cependant beaucoup moins que la convention classique de l'orbe, pour laquelle la nuance entre une conjonction limite et une conjonction exacte est laissée à l'entière subjectivité de l'astrologue.
Nous pouvons maintenant définir ce que nous qualifions de planète à forte concentration d'aspects:
Pour chaque planète i de chaque thème de naissance peuvent être calculées des concentrations d'aspects Ci, exprimés par les sommes des coefficients d'aspects Aij avec toutes les autres positions j du thème:
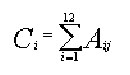
Par exemple, un thème comportant une double conjonction de mars (i=7) avec l'ascendant (4°, j=l) et avec vénus (8°, j=6) présentera une concentration de conjonctions martiennes égale à :
C7 = A7:1 + A7:6 = 0,25 + 0,5 = 0,75
Les planètes à forte concentration d'aspect sont donc celles qui obtiennent le score le plus élevé, et peuvent ainsi astrologiquement prétendre à la dominante du thème au titre de l'aspect en question (surtout la conjonction).
4. Méthode d'investigation statistique
Nous avons utilisé la loi des épreuves répétées de Bernouilli, qui converge vers une loi normale pour un nombre suffisant d'épreuves, et qui présente l'intérêt d'être à la fois simple et familière à toute personne ayant un jour étudié les statistiques, et d'autre part efficace du point de vue des probabilités.
Pour appliquer cette méthode, il est nécessaire de fixer le choix d'un paramètre jouant le rôle suivant: si le facteur de concentration des aspects s'appliquant sur une planète donnée dépasse ce seuil préétabli, la planète est considérée comme valorisée et l'épreuve comme réussie.
Ce paramètre dénommé seuil de concentration d'aspects planétaires a été choisi relativement bas (0.5) afin de ne pas avoir des probabilités (p) de dépassement trop faibles qui risqueraient de limiter la validité de l'approximation de la loi normale à de trop grands effectifs (N) de groupe. Remarquons qu'il ne doit pas être confondu avec une orbe, quoiqu'il s'y ramène dans le cas où une planète reçoit un seul aspect planétaire d'un type donné, ce qui, cependant, est le cas le plus fréquent.
La probabilité correspondant à une épreuve réussie pour un seuil égal à 0.5 est proche de la valeur 1/2 (ne confondons pas non plus ces deux valeurs! ), tel qu'en témoignent les résultats.
Or la loi normale peut être appliquée si:
N p (1-p) > 25
En ce qui nous concerne puisque p = 1/2 il est nécessaire que N > 100.
Le cardinal de nos groupes professionnels variant entre 125 pour les acteurs à 918 pour les médecins, nous pouvons donc, sans erreur qui ne soit négligeable, appliquer les formules de cette loi.
Nous proposons cependant d'utiliser ses tables de probabilité non seulement pour estimer les résultats de tous les groupes sur les scores de concentrations d'aspects, mais également pour estimer les résultats de certains groupes à effectif élevé sur les scores d'aspects individuels.
En effet, si nous choisissons le même seuil de 0.5 pour estimer qu'un aspect pris isolément s'applique ou non entre deux positions planétaires, nous obtenons, toujours d'après nos résultats, une probabilité de succès égale approximativement à 1/20. En reprenant l'inégalité mentionnée ci-dessus, nous calculons un cardinal minimal de groupe égal à 500, ce qui est le cas par exemple de nos groupes de musiciens et de médecins.
Remarque: un seuil de dépassement égal à 0.5 du coefficient d'aspect Aij correspond tout simplement à une orbe de validation d'un aspect égale à 16/2 = 8°' pour les conjonctions et les oppositions et à 8/2 = 4° pour les autres aspects.
5. Calcul des scores de référence par constitution d’épreuves aléatoires
Rappelons que l'essentiel de notre démarche repose sur ce calcul sur lequel nous consacrerons donc une grande partie de l'exposé.
Nous avons utilisé deux méthodes différentes de constitution de nos épreuves, reposant communément sur le calcul pour chaque étude de groupe de plus de 30000 échantillons de dates et heures pseudo-aléatoires, calculées selon un procédé qui tend à reproduire dans le fichier d'épreuves les mêmes distributions journalières, annuelles et séculaires de naissances que celles du fichier du groupe professionnel.
• 5.1 Première méthode
Etant donné une valeur Nd de dispersion choisie à l'avance, et un individu du groupe testé né à une date H0 / J0 / M0 / A0 , nous calculons une date H / J / M / A du groupe fictif :
1. H = H0 + alea(l) * Nd
2. J = J0 + alea(2) * Nd
3. M = M0 + alea(3) * Nd
4. A = A0 + alea(4) * Nd
où les aleas (k) sont des nombres aléatoires compris entre -1 et +1, et où J, M et A sont arrondies en valeurs entières afin d'obtenir de véritables jours, mois et années.
Ces calculs sont répétés pour les Np individus du groupe jusqu'à ce que le cardinal Nr du groupe de référence atteigne au moins la valeur 30000 (Nr = premier multiple de Np supérieur à 30000). Ce nombre a été choisi de manière à assurer une précision suffisante des scores moyens de référence, dont nous verrons plus loin le calcul d'erreur.
Commentons cependant le choix de la valeur de dispersion, que nous avons fixé à 4, pour la majorité de l'étude: en premier lieu, la question se pose de savoir pourquoi nous avons choisi la même valeur de dispersion pour l'heure, le jour, le mois et l'année, de même que la question de savoir pourquoi nous n'avons pas inclu par exemple les semaines ?
La réponse est le souci de respecter le maximum de simplicité dans un choix pour lequel se repose tout de suite le problème de l'action consciente ou non du chercheur sur les résultats de son travail, par sélection des données de départ.
Il est en effet tout à fait normal de nous suspecter d'avoir recherché les conditions initiales les plus favorables à un résultat que nous souhaiterions mettre en évidence.
Afin de lutter contre ce doute, nous avons préféré être critiqué pour ne pas avoir beaucoup réfléchi sur nos choix, en adoptant un paramètre de dispersion identique pour toutes les distributions, plutôt qu'être soupçonné d'avoir proposé une théorie erronée de la dispersion optimale dans le but d'aboutir à des résultats plus favorables.
Cela étant dit, il est important de vérifier qu'il est possible de donner une valeur à notre unique paramètre de dispersion, telle quelle permette d'éliminer les effets parasites mentionnés.
Considérons les trois effets principaux:
• 1) l'hétérogénéité des distributions journalières des naissances, dont la cause est principalement de nature sociale.
• 2) l'hétérogénéité des distributions annuelles: les naissances ont lieu plus souvent à certaines saisons.
• 3) l'hétérogénéité des distributions séculaires: les groupes professionnels sont choisis dans certaines générations, selon les sources de renseignements biographiques.
Nous considérons que la dispersion doit être choisie suffisamment petite devant la période de l'hétérogénéité globale, de manière à ce que l'allure de celle-ci se retrouve presque intégralement dans les groupes fictifs de référence. Cependant nous n'avons pas à restituer dans ces références les variations à plus haute fréquence de cette hétérogénéité, qui sont normalement dues au hasard. En bref, nous dirons que les distributions du groupe de référence seront les distributions lissées du groupe professionnel.
La dispersion que nous avons choisie (Nd = 4 unités) doit donc être comparée à la durée du jour (24) pour le premier effet, celle de l'année (12) pour le second et celle d'une génération (20) pour le dernier. Nous pouvons ainsi remarquer qu'elle est peut-être légèrement trop élevée en ce qui concerne l'effet saisonnier, c'est pourquoi nous avons effectué un second choix (Nd=2) pour lequel l'étude a été partiellement relancée et dont nous commenterons plus loin les effets.
• 5.2 Deuxième méthode
Dans cette autre démarche nous tirons la leçon des résultats obtenus par les différentes études menées avec la méthode précédente, qui confirment le problème pressenti de l'utilisation d'un facteur objectif de dispersion.
Le premier avantage de cette nouvelle méthode est d'éliminer toute intervention d'un paramètre d'entrée en utilisant pour la constitution des épreuves absolument les mêmes dates de naissance que celles du groupe professionnel, mais en mélangeant de façon aléatoire les éléments heures, jours, mois et années.
Considérons toutes les dates Hi / Ji / Mi / Ai du groupe de cardinal Ng ( i variant de 1 à Ng).
Les 30000 et quelques dates du fichier de référence sont alors constituées en tirant autant de fois 4 nombres aléatoires j, k, l, m compris entre 1 et Ng, et en formant ainsi les dates Hj / Jk / Mi / Am.
Le second avantage et principal intérêt de cette méthode est de rendre exactement similaires à celles du groupe professionnel les quatre distributions suivantes du groupe de référence:
• la répartition journalière des heures
• la répartition mensuelle des jours
• la répartition annuelle des mois
• la répartition séculaire des années
Par rapport à la première méthode, nous pouvons dire que la seconde reproduit en supplément dans le fichier de référence les variations à plus haute fréquence des courbes de distribution des groupes professionnels.
Sans aucun doute les trois effets parasites déjà mentionnés sont-ils ainsi efficacement balayés. Mais le revers de la médaille est que cette méthode contribue également à masquer une partie des corrélations dites astrologiques supposées être détectées, comme par exemple celles-ci:
le fait d'être né certaines années plutôt que d'autres à l'intérieur d'une génération donnée pourrait ne pas être uniquement du au hasard de l'échantillonnage biographique, mais également aux aspects de certaines planètes lentes.
le fait d'être né certains mois plutôt que d'autres pourrait aussi ne pas être seulement un phénomène saisonnier mais également conditionné par la période des conjonctions les plus fréquentes du Soleil, de mercure et de vénus avec certaines planètes lentes (!!!).
Cela dit notre philosophie est la suivante: mieux vaut trop corriger que pas assez.
Dans le premier cas nous sommes beaucoup plus certains, en présence d'un résultat, de sa qualité première. D'autre part, nous espérons qu'une simple égalisation des distributions ne devrait contribuer à éliminer qu'une faible partie des corrélations astrologiques, si astrologie il y a.
6. Précision des scores de référence
L'écart type d'un score d'épreuves répétées N fois et à probabilité de succès p est donné par:
![]()
Si nous appelons R le rapport entre le cardinal 30000 du groupe de référence fictif et le cardinal Np = 100 à 1000 du groupe professionnel étudié, l'écart type des scores de référence peut être exprimé ainsi:
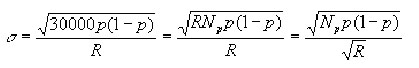
c’est à dire :
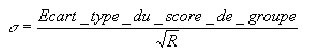
Nous pouvons alors estimer la précision relative de l'écart réduit du score de groupe de la façon suivante: prenons un intervalle de confiance du score de référence dont l'écart est le double ou le triple de son écart type, ce qui correspond à des probabilités très faibles de dépassement (resp. 0.02 et 0.001 dans un sens unique).
La précision de chaque écart réduit obtenu peut alors se chiffrer à:
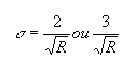
Selon la tolérance admise.
Prenons un exemple: nous trouvons un écart réduit de + 2.5 pour une planète d'un groupe de cardinal 300: il s'ensuit:
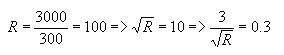
La vraie valeur de l'écart réduit est donc dans 5% des cas supérieure à + 2.3, et dans 1 pour 1000 cas supérieure à + 2.2. ( 2.5 - 0.2 et 2.5 - 0.3 )
Il est à noter que cette tolérance peut être encore diminuée en proportion de la racine du nombre d'études identiques et consécutives effectuées pour un groupe donné, en prenant comme écart réduit final la moyenne de tous les écarts réduits.
7. Groupes professionnels étudiés
Nous avons utilisé toutes les informations dont nous disposions et qu'il nous a été possible de rentrer sur ordinateur, et qui sont issues des publications suivantes de Michel Gauquelin:
1. New birth data series, volume 1:
• médecins
• militaires
• chefs d'entreprise
1. New birth data series, volume 3:
• écrivains
• artistes
• acteurs
• politiciens
• journalistes
1. Series A, volume 4:
• peintres
• musiciens
Nous n'avons cependant pas utilisé les peintres de cette dernière publication, faute d'avoir eu le temps (ou le courage!) de saisir tout le volume sur ordinateur. D'autre part, nous nous sommes limité aux professionnels nés en France, n'ayant pas encore à notre disposition de fichiers informatiques contenant les informations de décalages horaires ailleurs que dans ce pays.
8. Sélection des résultats présentés
Les résultats les plus significatifs ont été trouvés sur les concentrations de conjonctions, ce qui est déjà un résultat en soi puisque ces aspects sont considérés de loin comme les plus influents en astrologie.
Les tableaux de résultats complets étant très encombrants et par conséquent difficiles à analyser objectivement, c'est une raison supplémentaire pour laquelle nous avons présenté essentiellement les résultats concernant les conjonctions.
9. Organisation des calculs effectués
Cinq études ont été effectuées pour presque chaque groupe professionnel: les études 1 à 4 appliquent la première méthode de constitution des épreuves aléatoires, l'étude numéro 5 applique la seconde méthode:
1. 1) L'étude El a été menée avec les paramètres suivants:
• Seuil = 0,5
• Dispersion = 4
Des résultats complets en sont fournis pour tous les groupes professionnels.
Dans les études suivantes nous ne sont présentons que les écarts réduits des scores de concentration, pour ne pas surcharger le lecteur de colonnes de chiffres.
D'autre part elles n'ont été effectuées que pour les groupes professionnels ayant fournis des résultats significatifs dans la première.
1. 2) L'étude E2 a été menée avec les mêmes paramètres que précédemment, ayant eu pour objectif de vérifier que les résultats convergeaient approximativement vers les mêmes valeurs que dans l'étude 1.
2. 3) L'étude E3 a été menée avec un seuil de concentration réduit de moitié (0,25) et une dispersion inchangée pour observer l'effet induit sur les résultats des études 1 et 2.
3. 4) L'étude E4 a été menée avec le seuil initial (0,5) et avec une dispersion réduite de moitié (2) pour observer également l'effet induit sur les résultats des études 1 et 2.
4. 5) L'étude E5, qui applique une méthode différente de calcul, reprend la valeur originale du seuil (0.5), celui-ci devenant le seul paramètre de toute l'étude.
10 Contenu des tableaux de résultats
Les dernières pages contiennent des tableaux de résultats obtenus pour chaque groupe professionnel, divisés en cinq paragraphes:
1. I - Des tableaux complets des scores de conjonctions sont fournis pour la première étude. Ils sont à double entrée i et j à l'intersection desquels se trouvent deux nombres:
• celui du dessous représente le score de référence (ou score attendu) de l'aspect i.-j, calculé par moyennage des scores d'aspects aléatoires;
• celui du dessus représente l'écart du score de groupe de l'aspect i : j par rapport au score de référence précédent.
Viennent ensuite plusieurs tableaux à simple entrée:
1. II - les scores de concentrations: la première ligne, celle des conjonctions, représente en quelque sorte le cumul des lignes du tableau précédent, quoiqu'ils ne sont pas obtenus par addition mais selon la méthode des concentrations expliquée dans les pages précédentes. Les scores de concentration des autres aspects ont été indiqués dans les lignes suivantes.
2. III - les écarts réduits: ce sont les résultats finaux directement interprétables. Ils sont calculés en divisant les écarts des scores de concentration par l'écart type associé à chacun de ces scores, qui est lui-même obtenu de la façon suivante:
• a) la probabilité de succès p est calculée en divisant le score de concentration de référence par le cardinal Ng du groupe.
• b) l'écart type s'obtient par l'expression:
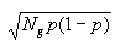
1. IV - Lorsque la première étude a donné des résultats positifs sur les conjonctions (ce qui est le cas pour la moitié des groupes professionnels), les tableaux des écarts réduits obtenus dans les études ultérieures 2 à 5 sont indiqués ensuite avec tous les aspects.
2. V - Dans ce dernier tableau sont donnés les écarts réduits des scores de concentration de conjonctions pour les 5 études des groupes professionnels sélectionnés: ils contiennent donc les résultats les plus intéressants de tout notre travail.
Pour estimer le degré de signification d'un écart réduit donné, voici un petit tableau qui fournit les probabilités d'obtenir un écart supérieur au nombre proposé:
| Ecarts | 1.28 | 1.64 | 2.05 | 2.32 | 2.57 | 2.88 | 3.09 |
| Probabilité | 0.1 | 0.05 | 0.02 | 0.01 | 0.005 | 0.002 | 0.001 |
| Inverse proba | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
ATTENTION
************
Un écart réduit compris entre - 1 et + 1 n'ayant pas la moindre signification, nous avons tout simplement annulé tous les résultats situés dans cet intervalle afin d'alléger les tableaux et de faciliter l'interprétation.
************
11. Hypothèses astrologiques Préliminaires
Les prévisions que nous avons fait avant étude sur les résultats des calculs s'inspirent de deux sources différentes:
1. Les travaux effectués par Michel Gauquelin:
Ce dernier a mis en évidence des corrélations très significatives entre les heures de la naissance de certaines notabilités professionnelles et les proches levers ou culminations de certaines planètes.
Cependant, notre méthode d'investigation utilisant les aspects planétaires, nous n'avons pas à reprendre nécessairement les mêmes relations planète / profession.
1. Les prévisions de la communauté astrologique:
Les travaux de Michel Gauquelin confirmant dans une certaine mesure le symbolisme astrologique, il est normal d'attribuer un certain crédit à priori à ce dernier. Aussi nous nous attacherons notamment à découvrir une éventuelle intervention des planètes que M.G. a mis à l'écart, pour deux raisons :
• elles n'ont apporté aucun résultat significatif dans ses statistiques.
• elles sont comme par hasard les plus lointaines ou les moins massives, ce qui accréditerait la version de l'influence physique.
Ces planètes sont mercure, uranus, neptune et pluton.
Nous avons donc inclus deux d'entre elles (mercure et neptune) dans les hypothèses suivantes que nous avons formulé ainsi:
| Groupe professionnel | planètes + | planètes - |
| Politiciens | Jupiter | |
| Acteurs | Jupiter | |
| Chefs d'entreprise | Mars et Jupiter | |
| Militaires | Mars | Lune et Vénus |
| Médecins | Mars et Saturne | |
| Ecrivains | Lune et Mercure | Mars |
| Journalistes | Mercure et Lune | |
| Artistes | Vénus | Mars et Saturne |
| Musiciens | Vénus et Neptune |
12. Résultats et commentaires
Afin de juger globalement des résultats, une première synthèse rapide peut être effectuée:
Sur l'ensemble des groupes professionnels testés (9), la moitié (4) fournissent des résultats intéressants, la moitié de ces derniers résultats (2) étant conformes aux hypothèses: il s'agit des musiciens (vénus et neptune) et des politiciens (jupiter). Les résultats non conformes sont ceux des militaires (mercure) et des écrivains (vénus).
Réunissons les écarts réduits dans un tableau synthétique:
| Etude | Musiciens | Musiciens | Politiciens | Ecrivains | Militaires |
| Vénus | Neptune | Jupiter | Vénus | Mercure | |
| 1 | 2.5 | 2.4 | 2.34 | 3.32 | 2.27 |
| 2 | 2.49 | 2.44 | 2.42 | 3.06 | 2.37 |
| 3 | 2.44 | 2.07 | 2.41 | 3.28 | 2.88 |
| 4 | 2.4 | 1.58 | 1.77 | 3.29 | 2.28 |
| 5 | 2.47 | 1.61 | 1.87 | 2.57 | 2.04 |
Voyons maintenant le crédit que nous pouvons attribuer à ces résultats, indépendamment de leur signification réelle, d'après les études successives qui ont été menées:
L'étude numéro 2 confirme bien les résultats de l'étude numéro 1, à une faible erreur près prévue dans nos précédentes estimations de la précision des résultats.
L'étude numéro 3 dans laquelle nous diminuons le seuil de 0.5 à 0.25 maintient bien chaque résultat et en augmente même certains très sensiblement. Nous pouvons donc conserver le seuil précédent sans avoir à douter d'avoir peut-être effectué un choix qui soit le seul profitable.
L'étude numéro 4 révèle que nous avons exagérément diminué le facteur de dispersion au moins en ce qui concerne la correction de génération, car elle effondre le score des deux planètes les plus lentes du lot, c'est-à-dire neptune et jupiter, contrairement aux deux autres planètes rapides mercure et venus dont les résultats se maintiennent.
Les groupes professionnels des musiciens (neptune) et des politiciens (jupiter) s'étalent en effet sur plusieurs générations, ne justifiant plus en ce qui les concerne le choix d'une si faible valeur du paramètre de dispersion séculaire. Il se confirme en fait que les individus des deux professions citées auraient eu tendance à naître tout à fait par hasard certaines années où les conjonctions avec les planètes jupiter ou neptune ont été plus fréquentes:
astrologie ou pas, c'est un fait.
Nous en déduisons également que le facteur de dispersion précédent (4) n'a pas été trop surestimé en ce qui concerne la dispersion annuelle des naissances.
L'étude numéro 5 nous fournit des résultats très satisfaisants compte tenu des remarques précédemment faites à propos du risque de la seconde méthode d'éliminer une partie de l'effet recherché: à part l'effondrement du score de Vénus chez les écrivains à une valeur malgré tout élevée, les autres résultats se confortent parfaitement et rejoignent les précédents, sans être aussi faibles cependant, ce qui nous semble très intéressant.
L'ensemble des études apportant des résultats cohérents entre eux et sans écarts excessifs, nous proposons avant de juger de leur véritable signification de nous référer dorénavant à leurs moyennes, même si cela n'est pas tout à fait rigoureux:
| Musiciens | Musiciens | Politiciens | Ecrivains | Militaires | |
| Vénus | Neptune | Jupiter | Vénus | Mercure | |
| Ecart réduit | 2.46 | 2.02 | 2.16 | 3.10 | 2.37 |
| Seuil proba | 0.007 | 0.022 | 0.015 | 0.001 | 0.009 |
| nverse proba | 143 | 45 | 67 | 1000 | 110 |
Il convient cependant de diviser par 10 les seuils de probabilité des résultats des écrivains et des militaires, puisqu'ils ne sont pas conformes aux hypothèses.
En effet, il y une probabilité 10 fois plus grande de voir un seuil franchi par le score de l'une quelconque des 10 planètes que par le score d'une planète définie à l'avance.
Il en résulte que les résultats suivants sont plus objectifs:
| Musiciens | Musiciens | Politiciens | Ecrivains | Militaires | |
| Vénus | Neptune | Jupiter | Vénus | Mercure | |
| Ecart réduit | 2.46 | 2.02 | 2.16 | 3.10 | 2.37 |
| Seuil proba | 0.007 | 0.022 | 0.015 | 0.01 | 0.09 |
| Inverse proba | 143 | 45 | 67 | 100 | 11 |
13. Conclusion
Les résultats de cette étude ont été calculés à partir de données qui d'une part n'ont fait l'objet d'aucune sélection trompeuse ni par Michel Gauquelin ni par nous-même, et d'autre part ont été constituées indépendamment de notre propos d'en tirer une information révélatrice concernant les aspects astrologiques.
Nous avons insisté sur la manière dont nous procédions pour éliminer les différents biais dont peuvent être victimes les résultats de ce genre de statistique et espérons avoir convaincu notre lecteur de la nécessité et du bien-fondé des différentes démarches que nous avons adopté à cet effet.
Nous avons appliqué une méthode de calcul des scores, des probabilités et des erreurs qui est la plus répandue et la plus simple de manière à éliminer le maximum de doutes sur ce point.
Nous avons pourtant trouvé des scores anormalement élevés de certaines concentrations de conjonctions de planètes sur la moitié des groupes testés, et ceci malgré un nombre d'individus ne dépassant pas quelques centaines: Les paris d'échec sont dans ces différents cas de 11 pour 1, de 45 pour 1, de 67 pour 1, de100 pour 1 et de 143 pour 1.
Bien que ces chiffres n'atteignent pas des valeurs telles qu'on puisse en tirer la moindre certitude absolue d'avoir mis en évidence un phénomène inexpliqué, nous voyons là un grand encouragement à poursuivre ce genre d'investigations sur d'autres fichiers de groupes professionnels.
C'est cependant sans nul doute la constitution de ces fichiers qui représente le travail le plus fastidieux, le plus délicat et le plus discuté. N'ayant pas nous-mêmes la possibilité de constituer de tels fichiers, nous nous mettons à la disposition de tout lecteur ayant réuni objectivement un nombre suffisant de nouvelles données de naissance pour recommencer nos calculs sur ces données, afin de confirmer ou d'infirmer les résultats précédents.
(Travaux réalisés par P.G. le préfacier scientifique de mon ouvrage.)
Bien à vous
Le 19 janvier 2009.
Michel d'Aoste